※ 本アーティクルは,北海道大学理学研究院在職時に行った検討を元にしたものです.
はじめに
私は数学というやつがまったく不得手です.嫌いだと言っても良いのかも.遠い昔の話ですが,大学教養課程では,それが理由で危うく留年しそうになりました.再再試でなんとかお情けで通してくれたK先生,ありがとうございます.そういう私なので,この話を地質学雑誌ではじめて目にしたときは仰天したというか雷に打ちのめされたような気分になったのですが,じゃあどうすればよいのか?その時点ではまったく分かりませんでした.その後いろいろ自分なりに追究してみた結果が下のアーティクルです.でも “数学音痴” の私ですから,もしかするとまったく的外れというか,間違っているのかも...いや,きっと間違っている?!
あと,さらに言い訳ですが,言うまでもなく私は数学を扱った論文など書いたことがありませんので,以下の記述における数学・統計学的な表現や言い回しには,多くの不適切な点を含むと思います.なんとなく分かるだろうというレベルですので,ご容赦ください.
“組成データ” とは?
“組成データ”(compositional data)とは,値がすべて正で,その総和が定数注1)になる(=定数和)変数(Aitchison, 1986)です.地質学で用いられる数値データの多く注2)が該当すると言われています.
注1)必ずしも厳密な定数和でなくても良い(らしい).
注2)化学組成・モード組成など.
組成データは,実データに比べて次元が一つ少なく広がりは有限(=単体空間:simplex)となります.単体空間の統計的性質が実空間のそれと同一である保証は無い(というかむしろ,同一ではない,と言うべきなのでしょう).
下に示したのは,0 < X < 1, 0 < Y < 1 の範囲でランダムに生成した2次元データです.これを,X と Y の和が一定(1)になるように再計算してやると,組成データとなりますが,それを XY グラフにプロットしてやると,当然ながら X + Y = 1 の直線状に配列した1次元データとなってしまいます.
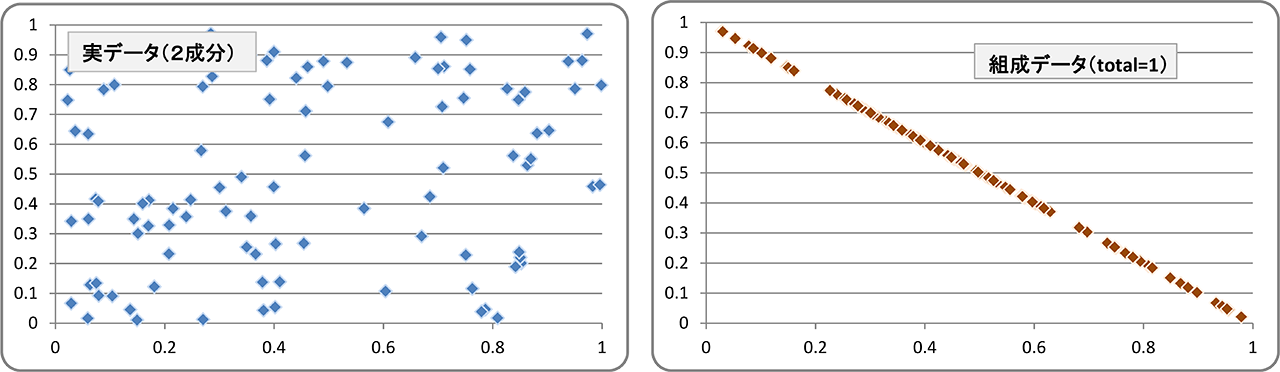
左:0 < X < 1, 0 < Y < 1 の範囲でランダムに生成した XY データ.右:そのデータを X + Y = 1 となるように再計算したもの.
ゼウスの雷(いかづち)

この “組成データ” という概念を私に初めて意識させたのは,太田・新井(2006)による地質学雑誌論文『組成データ解析の問題点とその解決方法』でした.それはまさに私にとって“ゼウスの雷(Zeus's Thunder)”でした.なぜそう感じたかというと,私は長年,砂岩組成研究者のはしくれとして砂岩のモード組成を扱ってきましたが,それがまさに “組成データ” そのものであったわけです.
そして太田・新井(2006)には,Aitchison (1986), Aitchison and Egozcue (2005) からの引用として,『これほどまでに混乱と解析方法の誤用が実行されてきたデータ形式は組成データ以外には見られない.さらに事態を深刻にしているのは,長い年月をかけた誤用の惰性によって,この誤用自体が現在では定常化してしまったという事実であろう.』という雷の如き言葉が記されていました.
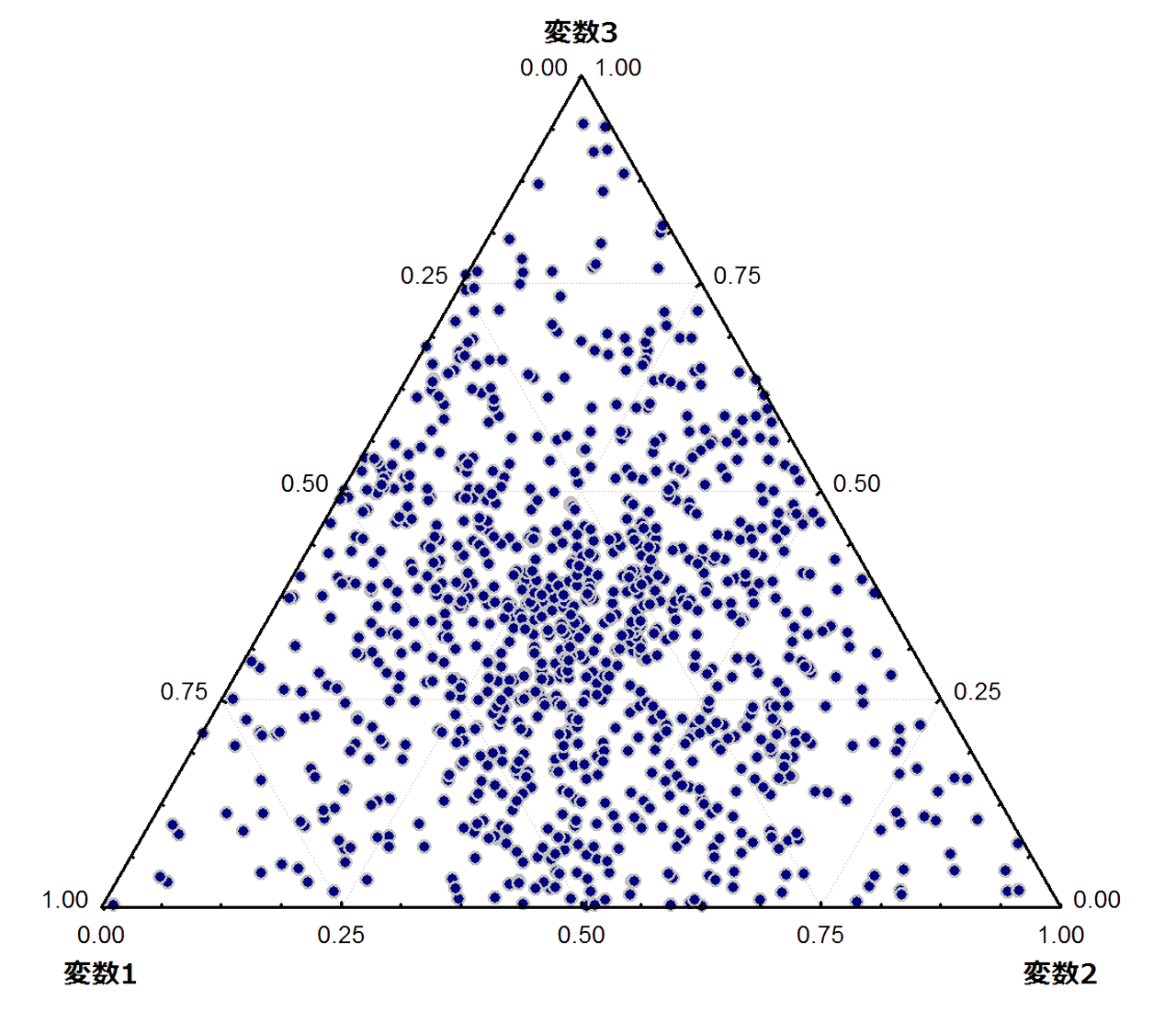 コンピュータで生成した3変数からなるランダムデータを三角図上にプロットしたもの.N = 1,000.
コンピュータで生成した3変数からなるランダムデータを三角図上にプロットしたもの.N = 1,000.
今まで私は長い間,砂岩のモード組成等を三角図上にプロットしてその統計的な傾向を論じてきたわけですが,それはすべて『混乱と誤用』だったのだということになるのです.
右に示したのは,三つのランダムな変数からなるデータを三角図上にプロットしたものです.変数1~3はランダムに生成したものなので,それらの中に統計的に有意な傾向は存在しないはずですが,三角図上では中央部に集中する明らかな傾向が認められます.これがつまり“実空間の統計的性質が単体空間のそれと同じとは限らない”という例になると思います.
例えばこれが砂岩の QFL モード組成だとすると,『XX層の砂岩モード組成は,Q=F=L の組成点を中心とした領域に集中する特徴を持つ』などという統計的フェイクにもなりかねない...
対数比変換法
これは,何とかしなくてはいけない...と思ったわけですが,太田・新井(2006)を読んでも,じゃあどうすればよいのか私にはさっぱり分かりませんでした.“なにか変換処理プログラムかワークシートでも太田・新井さんが配布してくれるのかな?” などと勝手に都合よく解釈したのですが,そういう気配もありません.
実は私の数学力の悲惨さの故に分からなかっただけで,その論文にちゃんとやり方が書いてあったのでした.私がそれに辿り着いたのは,ある契機のあった 2015 年暮れになってからで,その論文を読んでから実に 10 年近くが経過していました...(sigh)
alr 変換と clr 変換
 Aitchison (1986) による alr(X) と clr(X) の数式表現.
Aitchison (1986) による alr(X) と clr(X) の数式表現.
組成データの制約を解消する(=実データ空間に戻す)一つの方法として,『対数比変換(log-ratio transformation)』があります.
対数比変換にもいくつか種類がありますが,分かりやすいものとして,“相加対数比変換(additive log-ratio transformation: alr)” と “有心対数比変換(centered log-ratio transformation: clr)” の二つがあります(Aitchison, 1986).これらの数式表現を右に示します.
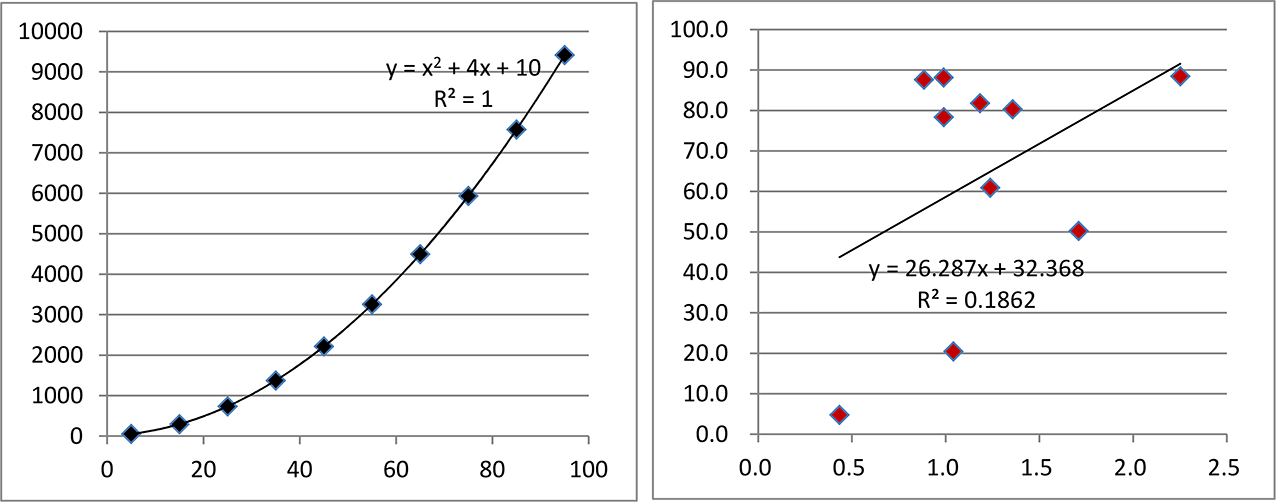 砂糖と塩の相関関係.グラフの縦軸 y が塩,横軸 x が砂糖.左:適当に二次相関関係を設定したもの.右:それにランダムに水と小麦粉を加え,総計を100として再計算し組成データ化したもの.
砂糖と塩の相関関係.グラフの縦軸 y が塩,横軸 x が砂糖.左:適当に二次相関関係を設定したもの.右:それにランダムに水と小麦粉を加え,総計を100として再計算し組成データ化したもの.
ここに,砂糖と塩と小麦粉と水の混合物(なんだそれ)があったとします.砂糖と塩は,ある相関関係(ここでは2次式による相関)を持っていますが,小麦粉と水は他の要素と相関がなく,系中にランダムに加えられるものとします.
砂糖と塩の XY グラフ(左図・左)はもちろん両者の完全な相関を示していますが,そこに小麦粉と水を加えて全体を100として再計算(組成データ化)すると,砂糖と塩との間に相関関係はまったく見られなくなります(左図・右).
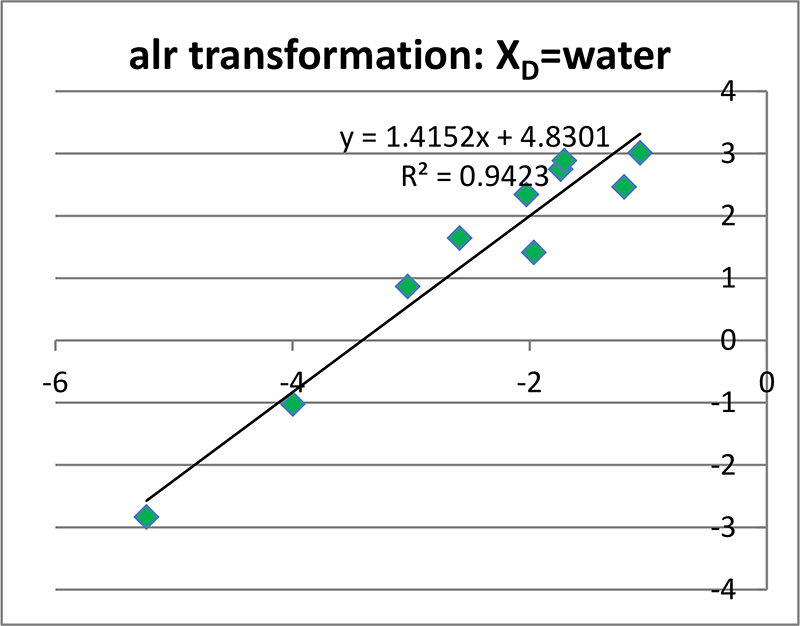 組成データ化したものに alr 変換を施した結果.良好な正の相関関係(R2 = 0.9423)が示されている.
組成データ化したものに alr 変換を施した結果.良好な正の相関関係(R2 = 0.9423)が示されている.
この組成データに対して alr 変換を行うと,砂糖と塩との間の相関関係が再びきれいに見えてきます(右図).なおこの場合の XD として水を使っています.“相関関係が再び見えてきた” とは言っても,その相関は元のデータの二次相関(上図・左)とは違って一次相関になっています.まあそれは対数比変換後なので,当たり前なのかな?とは思うのですが,私にはそれ以上のことは分かりません.
alr 変換と clr 変換の比較
対数比変換法の主な二つの方法について上に述べたわけですが,この二つの方法による変換結果は実際比べてみてどうなんでしょうか?
下にあげたのは,上の “砂糖塩小麦粉水混合物系” について,alr 変換と clr 変換をやってみた結果です.alr 変換結果については上にあげた結果と微妙に違っていますが,これは“ランダム関数の再計算によるもの”ですので,気にしないでください.
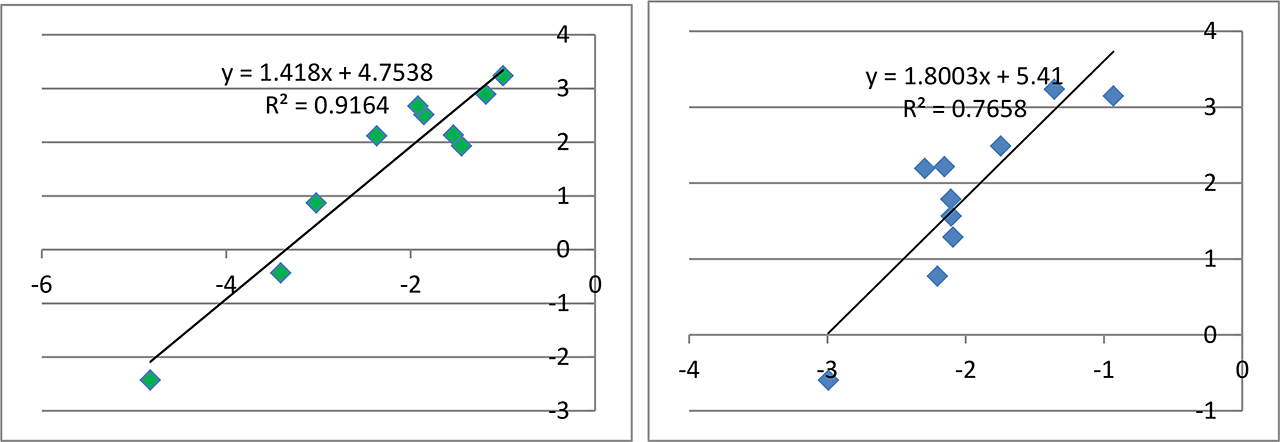
左:alr 変換結果.右:clr 変換結果.
で,『どっちも元の相関を復元できている』ということになると思います.ただ,clr 変換の結果は R2 がちょっと低いかな?という感じです.この例だけではなく,いろいろやってみた感じでは,alr 変換に比べて clr 変換による “復元度” がなんとなく低いような印象を受けました.統計学的根拠は分からないのですが.
まあ計算方法もちょっと複雑になるので,変数が一つ減っても良いのであれば,alr 変換を使うのがベターなのかな?と思っています.
alr変換における XD 問題
alr 変換法には,一つは,ある変数を XD として変換の分母に使ってしまうため,変換結果として使用できる変数は元の変数から一つ減ってしまうという問題があります.そのため,XD として使う変数は,『以降の統計的データ考察には使わないような』変数を使用するのが現実的でしょう.この制約は clr 変換にはないので,どの変数も考察から外したくない場合には clr 変換を使うのが妥当でしょう.
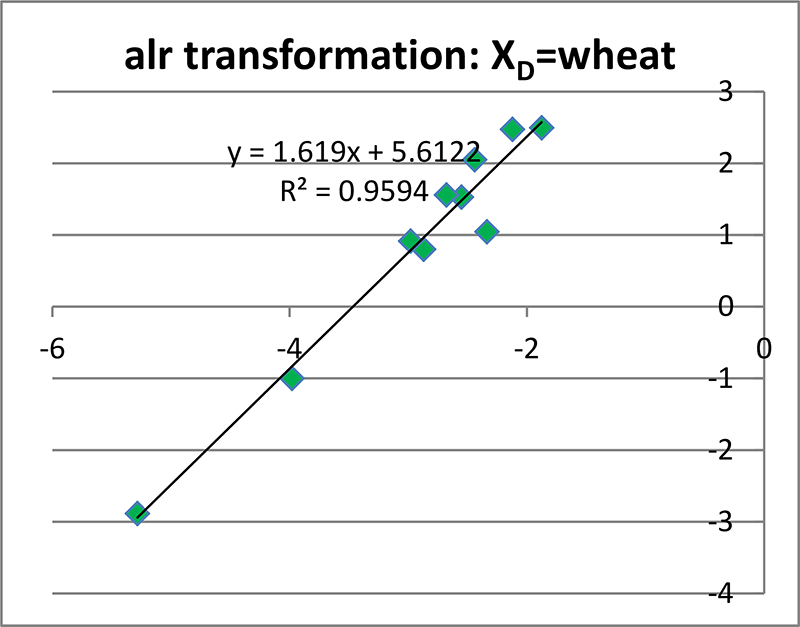
もう一つ,alr 変換を使う場合に誰もが気になるのは,“分母の XD として,いったいどの変数を使えば良いのか??” ということでしょう.結論から言うと,太田・新井(2006)に述べられているように,『どれを使っても統計学的には同じこと』なので,どれでも良いということになります.そのへんを上のデータを使ってちょっと検証してみました(左図).
この例は,XD として小麦粉を使ってみたものですが,たしかに上で示した水を使った変換結果とほとんど変わらない結果が得られました.どれを使っても良いんだということで,悩む必要がなくなりますので一安心です.
対数比変換におけるゼロ値問題
対数比変換の式を見て気づく人はすぐに気づくと思いますが,分子がゼロ(あるいは欠損値)だと,その対数を取ると当然エラーとなってしまいます.それではどうしたらよいかというと,私は勝手な判断でゼロ値を結果に影響を与えない程度に小さな数(例えば 0.001 とか)で置き換えていました.まあそれでも良いわけなんですが,太田・新井さん達はちゃんとその解を提示しています(新井・太田,2006;『組成データ解析における0値及び欠損値の扱いについて』).
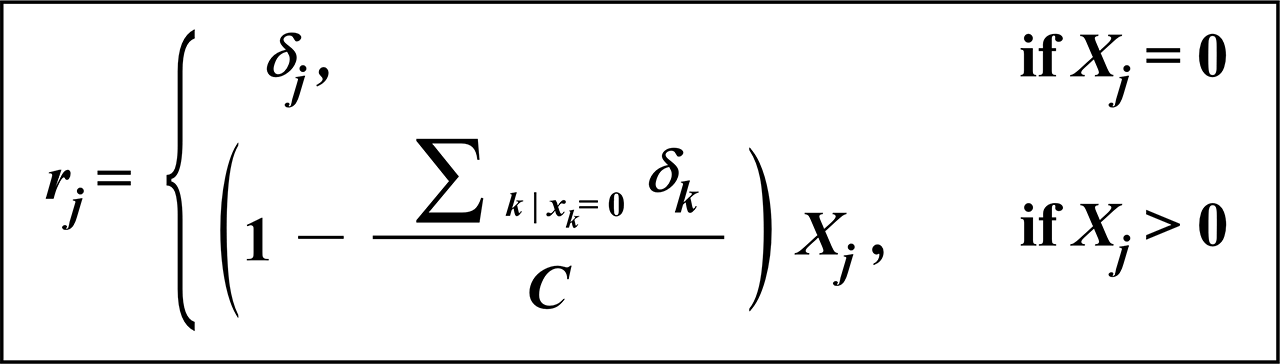 C:組成定数和.δj:0値置換の推定値≒測定誤差.
C:組成定数和.δj:0値置換の推定値≒測定誤差.
その内容の詳細はとても私には説明(理解)できないのですが,結論だけは明白です.つまり,Martin-Fernández et al. (2000, 2003) による “乗法置換法(の一つ)” を使えば良いということです.その方法は右の式で表されています.
実際のゼロ値置換の方法は,簡単に言うと以下のようになります.
① ゼロ値を測定誤差にあたる数で置き換える.例えば砂岩モード組成の場合,最小カウントである “1” で置き換える.
② 他の値を,ゼロ値を1で置き換えた分変数のトータルが増えてしまうので,トータルが変わらないように再計算する.例えば,砂岩モード組成で計100個の測定数のうち1個がゼロ値だったとすると,1 - (1/100) = 0.99 を元の測定値に乗じてやる.
直感的にお分かりのように,砂岩モード組成のようなデータの場合,0置換のあとも結果はそれほど変わりません.それから,上に書いた “私が適当にやっていた0置換” は①をやっていただけだった,ということになります.
現実地質世界における適用例?
これまでいろいろと組成データの “実空間への復元” について述べてきましたが,地質屋としては一番気になるのは,『あれこれ難しいこと言ってるけど,実際の地質データについてほんとに有効なの?』という点でしょう.なんだかんだ言って結局今まで地質学分野で長年使われてきた “誤用の” 解析方法でいいじゃんということであれば,何の意味もありません.
自分の持っているデータでそれを検証できればベストだったんですが,残念ながらそういう好例はありませんでした.もともと自前データに対する解析追究度が低かったというべきなのか...
そこで,ここでは Hulka and Heubeck (2010) によるデータを勝手にお借りして,組成データ解析の有効性(?)を示してみたいと思います.
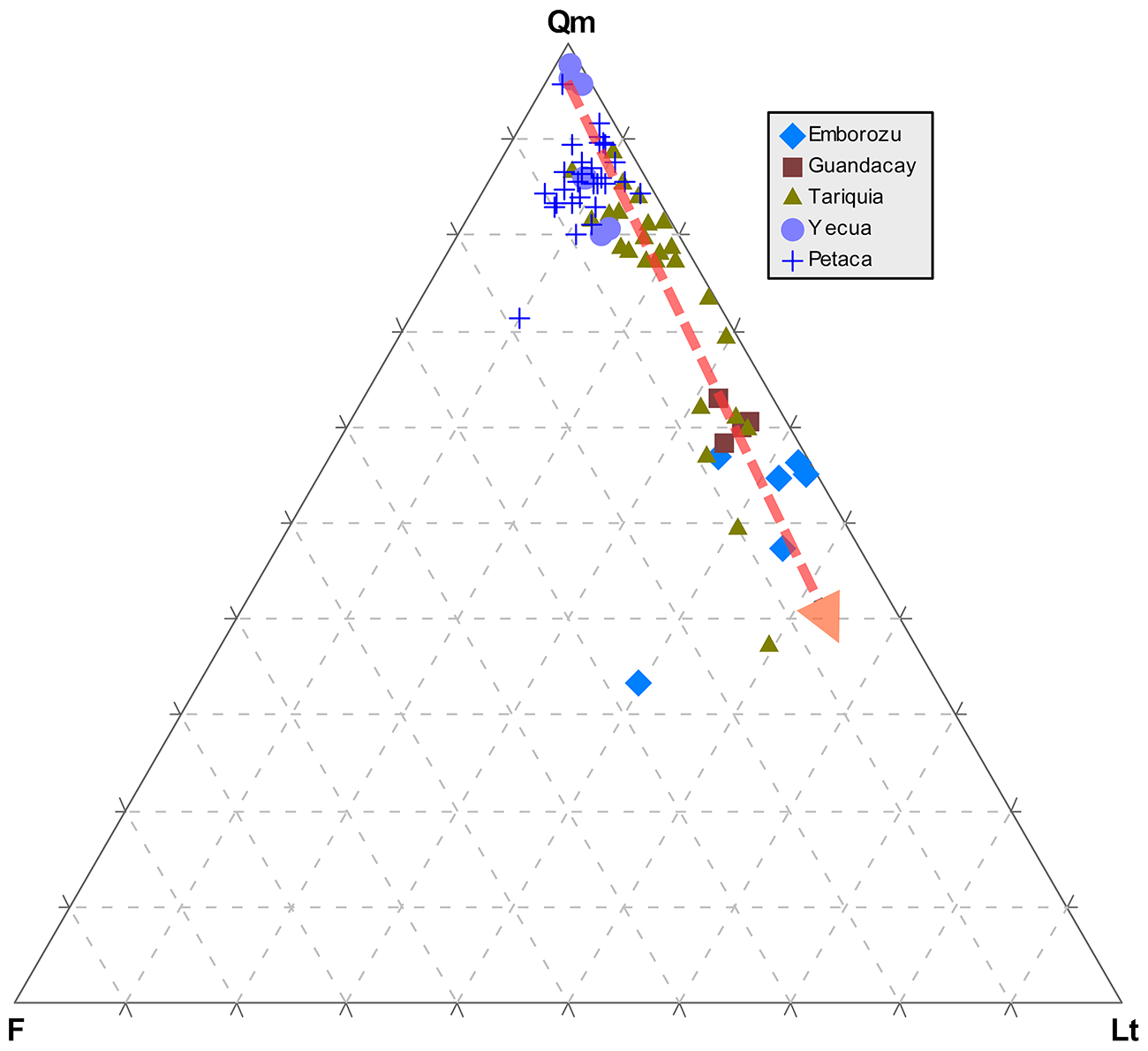 Huluka and Heubeck (2010) の砂岩モード組成を Qm-F-Lt 三角ダイアグラムにプロットしたもの.凡例は層名を表す.下位から,Petaca層(漸新世~中期中新世)→Yecua層(中期中新世~後期中新世)→Tariquia層(後期中新世)→Guandacay層→Emborozu層(後期中新世~現世).
Huluka and Heubeck (2010) の砂岩モード組成を Qm-F-Lt 三角ダイアグラムにプロットしたもの.凡例は層名を表す.下位から,Petaca層(漸新世~中期中新世)→Yecua層(中期中新世~後期中新世)→Tariquia層(後期中新世)→Guandacay層→Emborozu層(後期中新世~現世).
Hulka and Heubeck (2010: Composition and Provenance History of Late Cenozoic Sediments in Southeastern Bolivia: Implications for Chaco Foreland Basin Evolution and Andean Uplift, Jour.Sed.Geol.) は要約すると,アンデス山脈の東側前縁盆地の新生代堆積物の砕屑物組成から,山脈の上昇時期や過程を論じたものです.手法としては,ほぼ砂岩モード組成のみをを用いたオーソドックスなものです.ポイントとしては,砂岩組成が層位的上位に向かって石英-rich から 岩石破片-rich になっていくトレンド(右図:赤破線矢印)を見出し,そのことからアンデスの主要な上昇時期が中新世後期にあったという結論に達しています.この手法と結論はまったく妥当なもので,なんの問題もありません.なお,右図の凡例のところにあるのは層名で,凡例の上が上位になっています.
この三角ダイアグラムを見ると,たしかに層位学的上位に向かって Qm (monocrystalline Quartz) から Lt (Lithic fragments total) へ伸びるトレンドが見えています.よく見ると Qm-rich ドメインと Lt-rich ドメインとの間にはわずかにギャップがあるように見え,Tariquia 層はそのギャップにまたがっているようにも見えます.しかしそれ以上のことはよく分かりません.
このデータを,Qm-Lt 二成分図にプロットしてみたのが下図の左です.当然ですが,三角図で見るのと同様な傾向が見えていますが,それだけです.
そこで,このデータを alr 変換法で処理してみると,下図右のようになりました.
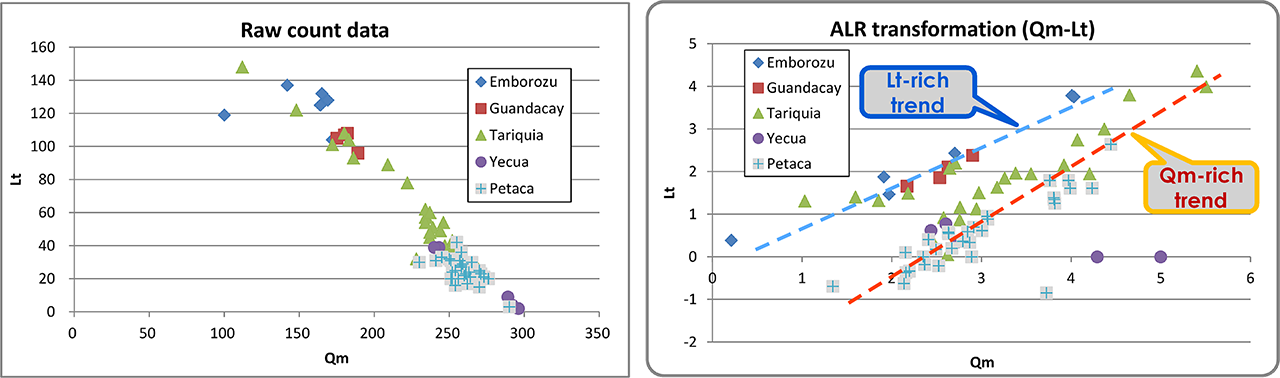
左:Hulka and Heubeck (2010) の砂岩組成の生データを Qm-Lt 二成分図にプロットしたもの.右:それらを alr 変換した結果.なお,alr 変換の XD には F(全長石)を使用している.
変換結果は,非常に目覚ましいものです.これらの砂岩モード組成は,Qm - Lt に関して,明瞭な二つのトレンド(Qm-rich and Lt-rich trends)を持っており,前者には下位層序(Petaca, Yecua),後者には上位層序(Guandacay, Embrozu)の砂岩が属しています.中位層準の Tarquia層は二つのトレンドに属していますが,それらはトレンド間にまたがっているのではなく,二つのトレンドに分離しているように見えます.Tarquia層の Lt-rich トレンドに乗っているサンプルの採取位置をチェックしてみると,いずれも研究地域の中央~北部に集中しており,Qm-rich トレンドに乗るものは南部地域のデータになっています.
これらのことは,①Tariquia-Guandacay の層序境界が diachronous であり,両層が同時異相の関係にある,②Qm-rich ⇒ Lt-richという供給変化が漸移的ではなかった(=ジャンプした)ことになり,なんらかのテクトニックイベントの存在を暗示する...という二つのことを示唆していると思われます.
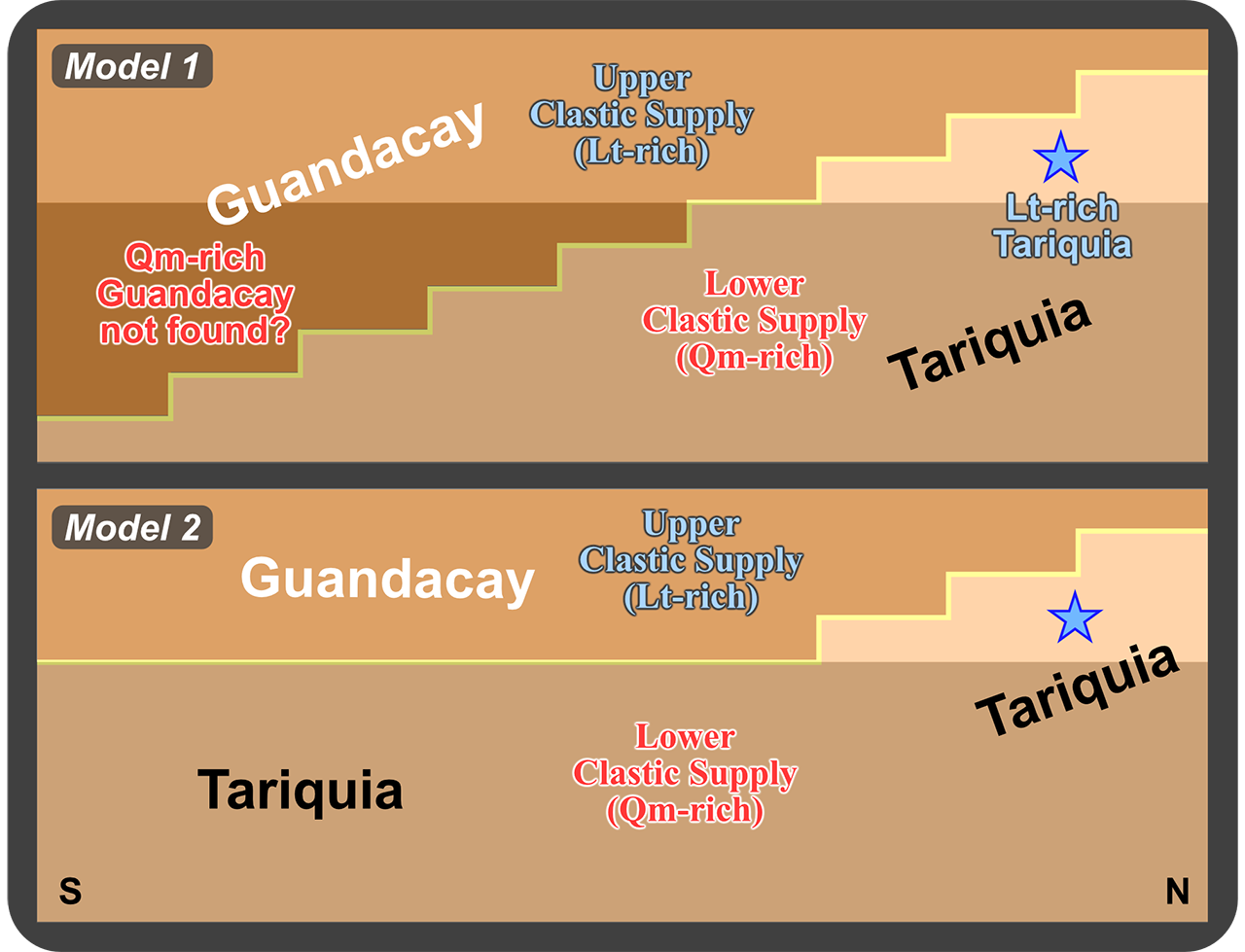
①についてのモデルを右図に示します.モデル1は,両層が単純に指交関係にあり Guandacay 層が Tariquia 層にオーバーラップしているというものですが,”Qm-rich な Guandacay” が見当たらないことを説明できません.そこで,両層の同時異相が少なくとも北部地域で部分的に見られるということであれば説明できるかもしれない,というのがモデル2です.
なお両層の指交関係は,Guandacay 層が S → N あるいは W → E の前進性堆積体であることを示すように見えます.
もちろんこういったことは,印刷された論文のデータだけを remote でいじっただけのものですので,本当にそういう地質学的可能性があるのかは,そのフィールドを調査した原著者しか検証することはできません.しかし,組成データの代表格である砂岩モード組成に対して対数比変換を施してみたらこれだけのことが新たに見えてきた,というのはやはりこの手法の有効性を評価するうえで実に興味深いことだと思われます.
(2019/04/15)(2024/02/08加筆)
付記(蛇足):本筋とは直接関係ない,老人の思い出話です.あれは私が北大理学部助手だった時のことだと思うので,もう30年近く前の話です.めっきり記憶が衰えているので,以下は,まったくの記憶違いかもしれませんが,その場合はご容赦.
当時私が所属していた『地鉱教室第2講座(層位学古生物学講座)』のK教授のところの大学院生だったY(or M?)君の研究発表が,たしか内輪の勉強会みたいな形で行われ,私も出席していました.その中で某礫岩の礫種モード組成(組成データですね)の話が出たのですが,“礫を何個か数えたデータが本当に砕屑物供給源の特徴を示すデータになりうるのか?” という趣旨の疑問が誰かから出ました.その時,そこにいたM助手の研究室の学生だったE君が,『何か適当な(花崗岩,だったか?)礫との個数比を出して議論したらどうか?』というアイデアを出しました.その時私はそのロジックの意義をあまり理解できなかったし,その話がその後どうなったかもまったく記憶にないのですが,今になって考えてみると,対数変換はしてないのですが,アイデアとしてはまさに “alr 変換” と共通した点があるのではないかと...
その後E君はM助手のもとで化石の構造変形を数学的に復元するという独創的な仕事をして博士号を取ったのではなかったかと思いますが...こんなこと私が言ってよいのかわかりませんけど,E君は “genius, gifted” だったのではないか?と密かに思っている次第です.まさか,Aitchison (1986) を既に読んでいたとか?! 科学の世界は恐ろしい...