ずっと下で,砂粒子の沈降シミュレーションの話書きましたが,その根幹に関わる話です.
私も確か学生の頃,粒子の沈降則としてストークスの法則というのを習いました.粒径の大きなものほど早く落ちるよ,というアレです.その式はまったく私のアタマに入っていませんでしたが,多くの教科書を見ると,こういう式が出てきます.
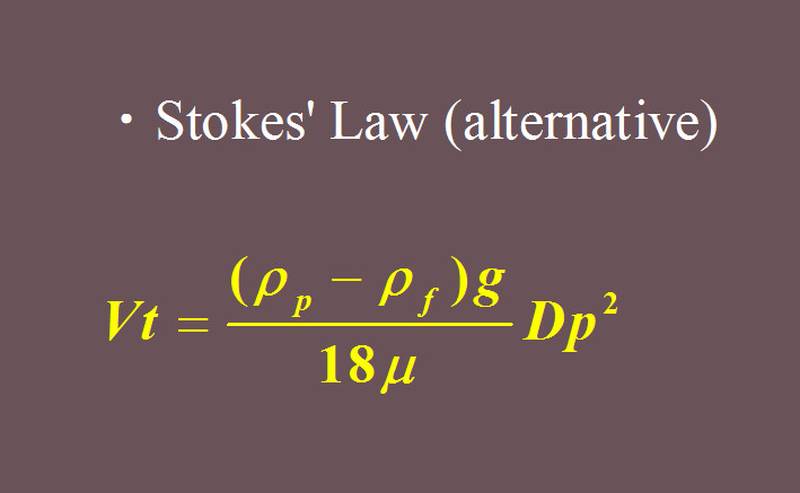
Vt:終末速度,ρp:粒子密度,ρf:媒質密度,g:重力加速度,μ:媒質粘性係数,Dp:粒子径,です.
これは電卓でも計算できるので,普通に使われています.しかし,Hsu の Physical Geology の教科書にもそういう挿話が出てきますが,シルトサイズくらいならまあまあでも,砂サイズ以上になると,『大砲の弾よりも速く沈降する』とからかわれています.
その点を解決するために,Gibbs の式というのが良く使われます.これはありていに言って,実験データから求められた多項式表現の経験式ということになると思います.
というわけで何を言いたいのかというと,私は学生のときからずっと,ストークスの法則って,原理はいいけど実際を表していない,と思っていました.
ところが最近,ネットで粉体工学関係のサイトにこんなストークス式を見つけました.
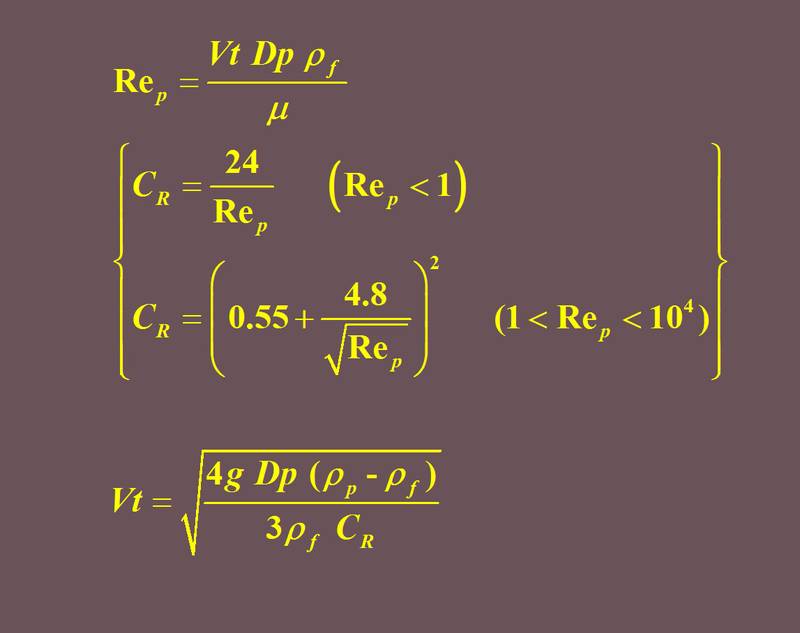
CRというのは抵抗係数で,レイノルズ数(Rep)をベースにしたもののようです.
この式は,両辺に Vt が入っているので,そのままでは単純に計算できません.ただし,Rep<1 の場合には,CR にこの式を代入してやると,結果として上の式(alternative)が得られます.Rep がそれ以外のときはおそらく無理だと思います.
で,計算して見ると分かりますけど,砂サイズ粒子の Rep は1を大きく上回っています.この辺が,Hsu の教科書で揶揄されているポイントだったんだなと思います.
というわけで,今回の粒子沈降シミュレーションでは,この方程式を解くのに反復法(iteration mewthod)を使って解きました.その結果が,このグラフです.
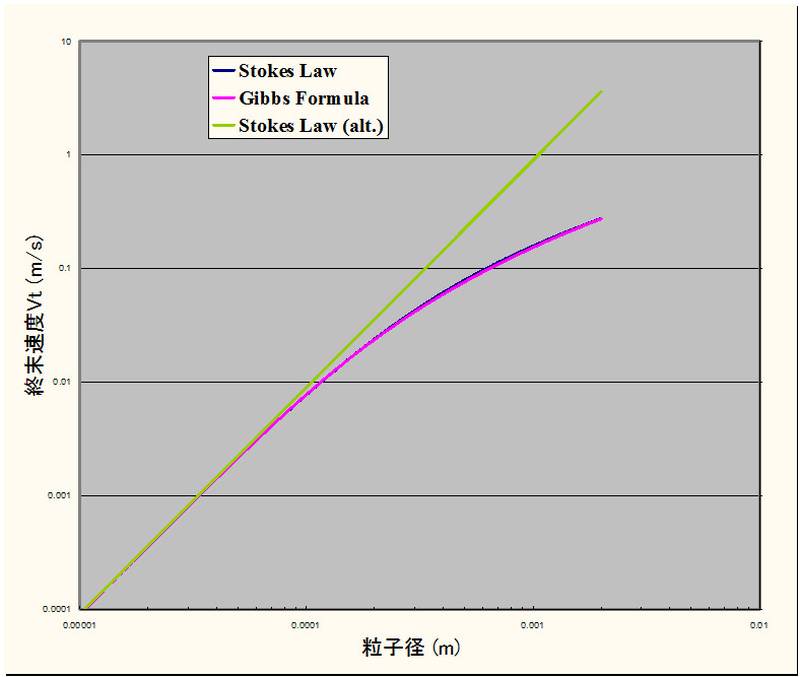
緑の線が一番最初に示した,普通出回っている電卓計算可能なストークスの式で計算したもの.両対数軸だとほとんど直線になります.
下のカーブが,重なっていて分かりにくいのですが,ピンクが Gibbs式によるもの,濃紺が上のストークス式を反復法で解いたものです.両者は実に良く一致していて,『理論式が現実とよくマッチしている』というハッピーな結果となっています.
そうか,そういうことだったんだな...と私はこの歳になって初めて理解できました.少なくとも理解できたような気がします.こういう自分が学生に講義で教える身だったとは...反省です.m(__)m